 AGAT stands for Algebraic Geometry and Approximation Theory. Approximation theory deals (in particular) with questions about the dimensions of spaces of splines. Here is
a very good write-up
about the field.
AGAT stands for Algebraic Geometry and Approximation Theory. Approximation theory deals (in particular) with questions about the dimensions of spaces of splines. Here is
a very good write-up
about the field.
Algebraic geometry is a branch of mathematics that studies connections between geometric properties of curves and surfaces defined by polynomial equations in an \(n\)-dimensional space and algebraic properties of the sets of polynomials that define the surfaces. You can check out this friendly introduction to some of the problems and methods of the field.
So what do the two subjects have in common? A short answer is: polynomials!
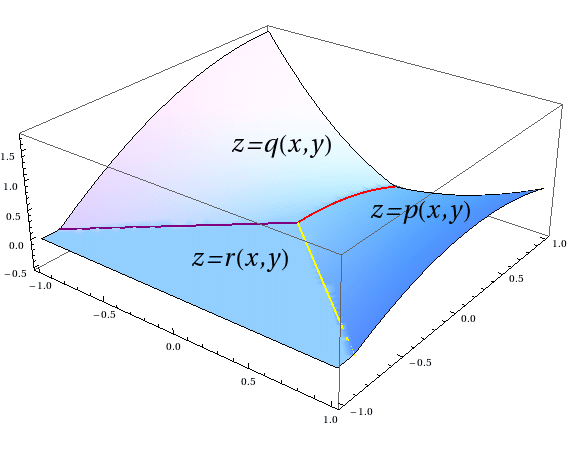
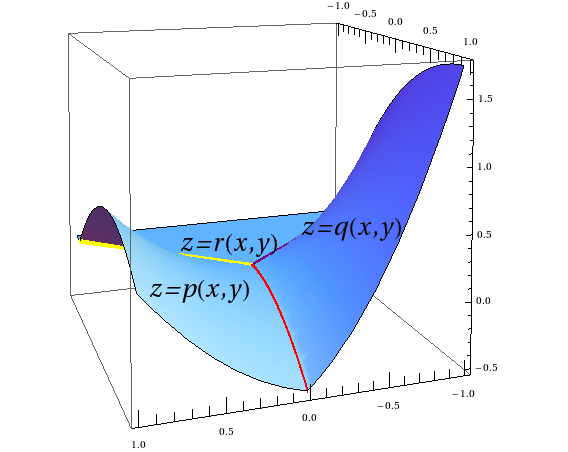 Splines are piecewise polynomial functions; you can see the graph of one above. The graph of same function, from a different angle, is shown on the left. The function in the images has three "pieces," each defined by a polynomial function, that are attached to each other along the three lines. Here, "attached" means that the values of the functions \(p\) and \(q\) must coincide along the red line,
\(q\) and \(r\) along the purple line, and so on.
Splines are piecewise polynomial functions; you can see the graph of one above. The graph of same function, from a different angle, is shown on the left. The function in the images has three "pieces," each defined by a polynomial function, that are attached to each other along the three lines. Here, "attached" means that the values of the functions \(p\) and \(q\) must coincide along the red line,
\(q\) and \(r\) along the purple line, and so on.
Often, more strict conditions (they are called smoothness conditions) are required: for example, that the partial derivatives up to a certain order are equal. It is clear from the picture that the functions \(p\) and \(q\) are not joined smoothly: there is a ridge running along the red line (in fact, there is a ridge along each of the three lines here).
It turns out that these smoothness conditions can be expressed in the language of polynomials and that the set of all piecewise polynomial functions (of all degrees) satisfying a fixed set of smoothness conditions forms a module over the ring of polynomials. The latter is an algebraic object that can be studied using the tools of commutative algebra.
My colleague Tatyana Sorokina and I have organized a mathematics activity group in AGAT. We see mathematics activity group as a venue, similar to a laboratory in a science field, that allows faculty and students to work on open problems that are of current interest to the specialists in the field. The students' role in the project varies depending on the level of mathematical sophistication and on the interest. Most of the students are exploring the dimensions of spline spaces using the tools such as applet developed by Peter Alfeld and Macaulay2 program.