Computer Algebra Systems (CAS) are frequently incorporated in mathematics classes at college level. The way I see it, the goal is two-fold: one, the students are able to visualize mathematical concepts and experiment with them; and two, software such as Mathematica is quite widely used, both in academia and in industry. Knowing how to interact with it and knowing at least some of the capabilities is likely to be useful.

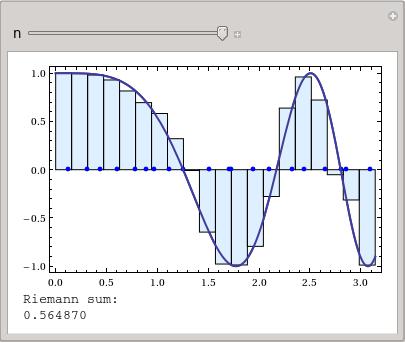
At Towson, all Calculus classes have a Mathematica lab component. The "notebook" files contain examples and exercises. Sometimes, I find it useful to go through the examples as a part of the lecture. A good example is an interactive plot visualizing the concept of the Riemann sum of a function, shown in the snapshot on the left.

The labs include brief summary of mathematical notions that are discussed, examples, and exercises that the students do on their own (with some help, obviously). For example, here are some excerpts from the lab on limits (hover over the image to see a larger version).

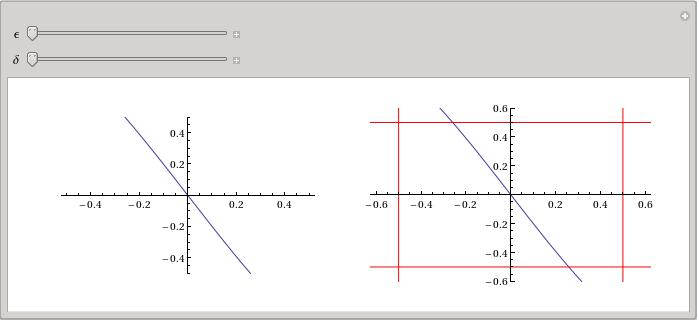
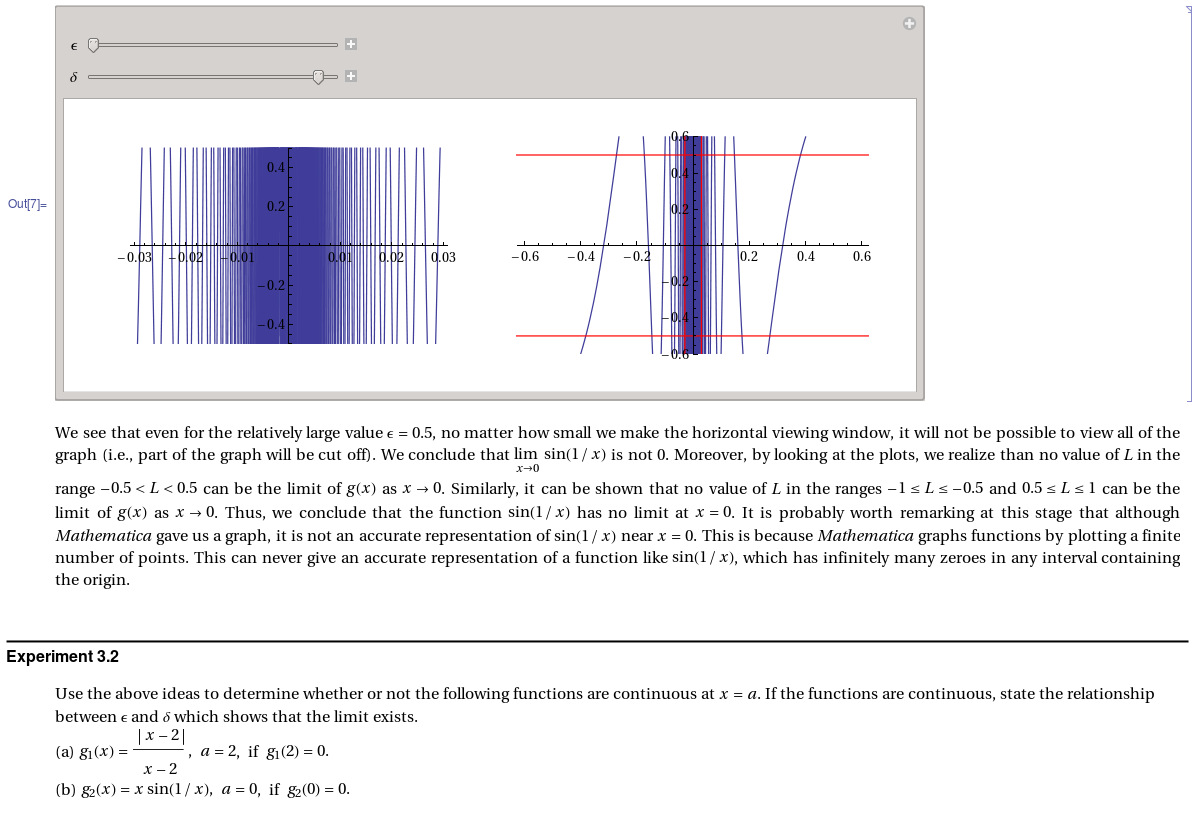
The main challenge (for me, at least) is to pick the right level of difficulty. If the lab exercises are "recipe-based", then they simply turn into the "busy work" for the students without much benefit. At the same time, when students struggle too much with syntax, coding, etc., it tends to distract them from the main goals of the course. A solution that works for me (more often than not) is to have exercises that are simple to execute in Mathematica (by running already written routines), but that ask the students to analyse and explain the information obtained from those routines.

I would be happy to share more information about the labs, please do not hesitate to contact me.