Organic Redox Reactions

OXIDATION STATE

To determine the oxidation state of simple inorganic compounds, you assume that the oxidation state of all but one of the elements in the compound is known and determine the remaining element by difference, since the sum of all oxidation number must be zero. For example, in KMnO₄, potassium is always +1, each oxygen is -2 (for a total oxidation number of -8) and thus the manganese must be +7.

A similar approach is taken in organic compounds, but a carbon is nearly always the unknown. Carbon atoms can have any oxidation state from -4 (e.g. CH₄) to +4 (e.g. CCl₄). If there is more than one carbon in the molecule, each needs to be calculated, but there are now several more unknown oxidation states than there are knowns to use in their determination. An useful solution to the problem can be generated by accepting two important facts:

an absolute value for the oxidation state cannot be determined.
only the changes in oxidation state during a reaction are important, so the absolute value isn't needed.

The approach described here calculates oxidation state in a consistent manner which always gives the correct oxidation state change for a reaction, and parallels the method used for KMnO₄ above.

Elements other than carbon are assigned their normal oxidation state: H: +1; O: -2; halogens: -1; and as a consequence OH: -1. There are easily recognized situations where these elements are known to have other oxidation states: hydrides such as LiAlH₄ (H: -1), peroxides such as H₂O₂ (O: -1), or the elements (Cl₂, H₂, O₂: 0).
Once the particular carbon of interest is chosen (the one that is changed during the reaction), all other carbons are assigned an oxidation state of 0 (even if you know otherwise)! The oxidation state of the carbon of interest is then calculated by the method used for an inorganic element like Mn in KMnO₄ above.

Examples:

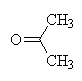
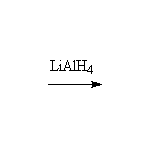
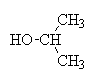In the reaction below, in which a ketone is converted to an alcohol, the only change in oxidation state occurs at the carbon with the oxygen; the method is outlined and shows that the carbon's oxidation state is reduced from +2 to 0, equivalent to addition of 2 electrons.

+ Li⁺ + Al⁺³

Acetone carbon oxidation states:

Carbon number	Attached atoms	Sum of oxn nos of attached atoms	C oxidation state
1	3H, 1C	3(+1) + 1(0) = +3	-3
2	2C, 1O	2(0) + 1(-2) = -2	+2
3	3H, 1C	3(+1) + 1(0) = +3	-3

2-Propanol carbon oxidation states

Carbon number	Attached atoms	Sum of oxn nos of attached atoms	C oxidation state
1	3H, 1C	3(+1) + 1(0) = +3	-3
2	2C, 1H, 1OH	2(0) + 1(+1) + 1(-1) = 0	0
3	3H, 1C	3(+1) + 1(0) = +3	-3

The same procedure can be used to determine the oxidation state of nitrogen in organic and inorganic compounds which varies from -3 (NH₃) to +5 (HNO₃); it occurs in all its oxidation states in organic compounds and it too can participate in redox reactions.

BALANCING EQUATIONS

To use these computations to determine the relative amounts of reagents needed to perform a chemical reaction, use these oxidation state changes as you did for inorganic reactions; the electrons donated by the reducing agent must be equal to the electrons gained by the oxidizing agent. For example, LiAlH₄, has a normal Li: +1, Al: +3, and abnormal H: -1, and reacts as follows (the products are shown after neutralization and isolation by water):

LiAlH₄ +

+ H₂O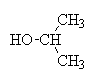

+ LiOH + Al(OH)₃

The Li: +1, Al: +3, O: -2 and the CH₃'s are unchanged by this reaction. Changed are C-2 and H. The half reactions, balanced, are:

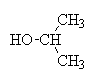
LiAlH₄

4H+ + 8e- + Li⁺ + Al⁺³

+ 2e- + 2 H⁺

We have determined that each LiAlH₄ can reduce 4 acetone molecules. To write a balanced equation, multiply the second equation by 4 and add the two equations.

+ LiAlH₄ + 4 H⁺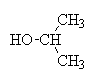

+ Li⁺ + Al⁺³

The H⁺ added to this reaction is an artifact of the procedure we used to balance the equation. We could have arbitrarily added 4 OH^- to both sides of the equation to generate one like that above. In fact, the reaction does not occur under acid or aqueous conditions. Reduction of the ketone can only be accomplished under absolutely anhydrous and acid-free conditions. If any water or acid is present, LiAlH₄ reacts with the acid or water to produce H₂. For this reaction, the acid and/or water is added after the LiAlH₄ and acetone have completely reacted. Remember that "balancing equations" is a kind of arithmetic that attempts to regenerate observed redox reactions using the numerical concept of oxidation state: just because we can balance a redox equation does not mean that it occurs. It is essential that the reagents and products be determined experimentally before checking the relative number of moles expected by "balancing the equation". In cases like this where the reaction is non-aqueous, it is more realistic not to insert any of the components of water on the left-hand-side, since they will not be in the reaction. The actual reaction, without neutralization, is:

+ LiAlH₄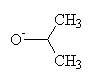

+ Li⁺ + Al⁺³

For practice, convince yourself that conversion of an alkyl halide to a Grignard reagent reduces the carbon by 2 electrons, and balance the equation for oxidation of an alcohol to a ketone by chromic acid. Keep this method in mind for biochemical redox reactions - it works just as well.

OTHER USES

This procedure described above can also be used to show that oxidation/reduction has not occurred, even when the oxygen content of a molecule changes. For example, addition of water to an alkene: CH₂=CH₂ + H₂O

CH₃-CH₂OH Oxidation states: for ethene: -2 , -2 ; for ethanol: -3 -1

In this case, the computation indicates a reshuffling of electrons within the molecule, making the two carbons different, but no overall oxidation. This should not be surprising, since water is not easy to oxidize or reduce (sodium metal can reduce it partially to H₂).

Click here to transfer to a list and some properties of some typical oxidizing and reducing agents.

ORGANIC ENRICHMENT, L. M. SWEETING, 1993, 1997