where M is the cation of charge n+ and X is the anion of charge n-. The subscripts of the salt become the coefficients for the ions. The equilibrium mass action expression would be:
Notice that only the aqueous ions are part of the mass action expression. Solids are never included. Also notice that the coefficient for each ion becomes the exponent in the mass action expression.
Solubility in pure water
Convert this equation into net ionic form by crossing out the spectator ions from the total ionic form of the equation:
Find the initial concentration of Ca2+ ions and PO43- ions:

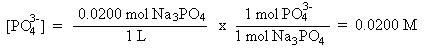
Next, determine the new, diluted concentration of the Ca2+ ions and the PO43- ions resulting from the mixing of the two solutions:
Calculate the solubility product quotient, Q, based on the mass action expression of the solubility equilibrium:
Compare the value of Q to the value of Ksp. If the Ksp > Q, then solubility has not been exceeded and a precipitate would not form. If the Ksp < Q, the solubility has been exceeded, and a precipitate would form. The Ksp of Ca3(PO4)2 is 1.0 x 10-26. Since Q, 6.532 x 10-12, exceeds the Ksp of 1.0 x 10-26, a precipitate of Ca3(PO4)2 will form in this case.
The Ksp of Ca3(PO4)2 is 1.0 x 10-26, and is either given in the problem or found on a table of solubility product constants. Below the equilibrium, show what is occurring initially, the change to establish equilibrium, and the conditions at equilibrium:
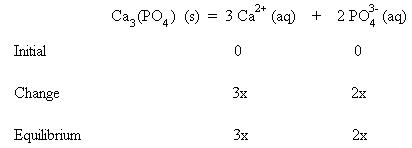
Initially, calcium phosphate has not dissociated, thus the concentrations of calcium ions and phosphate ions is 0. To establish equilibrium, some calcium phosphate must dissociate as a 3x amount of calcium ions and 2x amount of phosphate ions. Thus, at equilibrium, the amount of calcium ions is 3x, and the amount of phosphate ions is 2x. These values are substituted into the mass action expression:
As a reminder, Ca3(PO4)2 is a solid, and is therefore not a part of the mass actions expression.
Solve the above algebraic expression for x:
The value of x is the molar solubility of Ca3(PO4)2. The actual concentrations of Ca2+ ions and PO43-ions in solution is given by:
Using the molar solubility, one may calculate the actual mass of calcium phosphate dissolved in one liter of water:
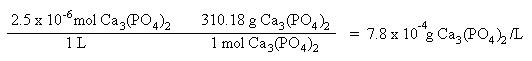
Solubility in the presence of a common ion
The lowered solubility of calcium phosphate becomes very evident when the problem is approached quantitatively. A typical problem would read:
The equilibrium taking place is:
Keep in mind that while excess phosphate will be present from the sodium phosphate, sodium ion is just a spectator ion during this process.
Set up an equilibrium table, as before:
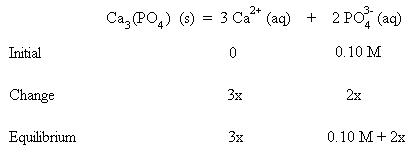
Notice how the initial amount of phosphate ion is not zero. This initial amount of phosphate ion is contributed by the 0.10 M sodium phosphate solution. For equilibrium to become established, a 3x amount of calcium ion is formed and an additional 2x amount of phosphate ion from the dissociation of calcium phosphate is introduced. Thus at equilibrium, the amount of calcium ion is 3x and the amount of phosphate ion is 0.10 + 2x.
Substitute the algebraic terms into the mass action expression:
The above expression is polynomial and its solution may require a serial approximation technique. However, solving for x may be simplified if the 2x term in the second factor may be neglected. Recall that the solubility, x, in pure water had a magnitude of 10-6. Comparing a magnitude of 10-6 to 0.10, one can see that 2x will be negligibly small, and thus can be neglected in the above expression. This simplifies the equation to:
Solve for x by dividing through both sides of the equation by 0.27:
Next, take the cube root of both sides of the expression:
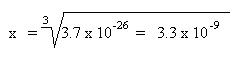
As one can see, x, the solubility is quite small. Our assumption to neglect the 2x in the original algebraic expression was valid. Also, one can quantitatively see how the solubility has decreased. In pure water, the solubility of calcium phosphate was 2.5 x 10-6; in the presence of a common ion, phosphate ion, with a concentration of 0.10 M, the solubility of calcium phosphate decreased to 3.3 x 10-9.
Selective precipitation
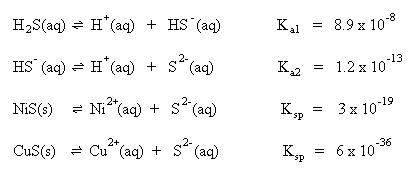
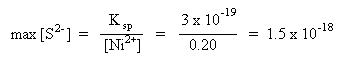
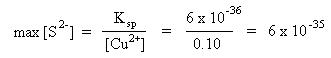
Nickel(II) sulfide is many times more soluble than copper(II) sulfide. If the sulfide ion concentration is set to the more soluble maximum sulfide ion concentration of nickel(II) sulfide, (1.5 x 10-18 M), copper(II) sulfide will precipitate and nickel(II) sulfide will remain in solution. The sulfide ion concentration is adjusted using a saturated hydrogen sulfide solution as a function of pH. Since hydrogen sulfide is a diprotic acid, there are two sources of hydrogen ions (H2S and HS-), as shown by the first two equilibria, above. It will be easier to solve for the hydrogen ion concentration, if only one mass action expression were involved. With this in mind, combine the two equilibria into one overall equilibrium:
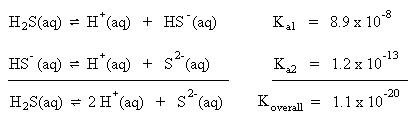
The mass action expression for the above equilibrium is:
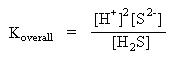
Rearrange the above equation to solve for the hydrogen ion concentration. Multiply both sides of the equation by the hydrogen sulfide concentration and divide both sides by the sulfide ion concentration:
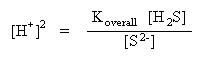
Take the square root of both sides of the equation:
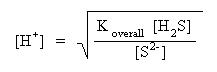
The concentration of a saturated solution of hydrogen sulfide is 0.10 M. For sulfide ion concentration, substitute the more soluble sulfide ion concentration calculated previously. Substitute for Koverall. Solve for hydrogen ion concentration:
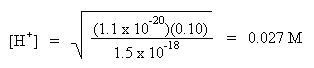
Finally, calculate the pH:
This pH represents the maximum pH which must be maintained in order to separate nickel(II) ions and copper(II) ions. Since the sulfide ion concentration is 1.5 x 10-18 M, the actual copper(II) ion concentration remaining in solution is:
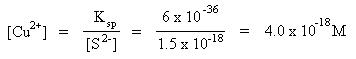
As one can see, the copper(II) ion concentration is indeed very negligible. The concentration of nickel(II) ions remains 0.20 M.
© Copyrght, 2001, L. Ladon. Permission is granted to use and duplicate these materials for non-profit educational use, under the following conditions: No changes or modifications will be made without written permission from the author. Copyright registration marks and author acknowledgement must be retained intact.