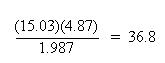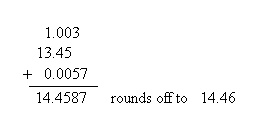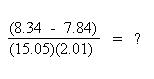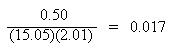Multiplication and division -- round the final result to the least number of significant figures of any one term, for example:
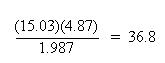
The answer, 36.8, is rounded to three significant figures, because least number of significant figures was found in the term, 4.87. The other terms, 15.03 and 1.987, each had 4 significant figures.
Addition and subtraction -- round the final result to the least number of decimal places, regardless of the significant figures of any one term, for example:
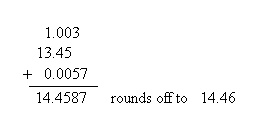
The answer, 14.4587, was rounded to two decimal places, since the least number of decimal places found in the given terms was 2 (in the term, 13.45).
Suppose more than one mathematical operation is involved in the calculation? Such a calculation may be "deceptive" as to how many significant figures are actually involved. For instance:
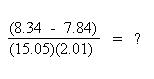
The subtraction in the numerator must be performed first to establish the number of significant figures in the numerator. The subtraction results in:
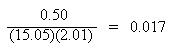
Since the subtraction in the numerator resulted in a number to two significant figures (rounding to two decimal places), and the least number of significant figures in the resulting expression involving multiplication and division is now two significant figures, the final result must be rounded to two significant figures.
Created With HTML Assistant Pro - 05/11/2001
© Copyrght, 2001, L. Ladon. Permission is granted to use and duplicate these materials for non-profit educational use, under the following conditions: No changes or modifications will be made without written permission from the author. Copyright registration marks and author acknowledgement must be retained intact.