Strong Acids and Strong Bases
Weak Acids and Bases
Dissociation of a Weak Acid
The equilibrium may be expressed mathematically by setting the Ka equal to the mass action expression:


Note that water will not be included in the calculation since is the solvent.
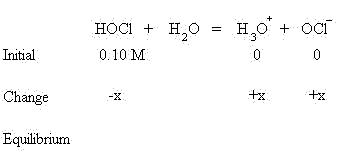

These quantities will be used in the mass action expression for the equilibrium of the acid, as shown below. The Ka for HOCl is 3.5 x 10-8.

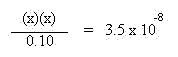
Multiplying both sides by 0.10 yields:
Taking the square root of both sides yields:
To find the pH, take the negative log of the hydronium ion concentration:
Incidently, the concentration of HOCl at equilibrium would be:
This shows our assumption that x was negligible was valid.
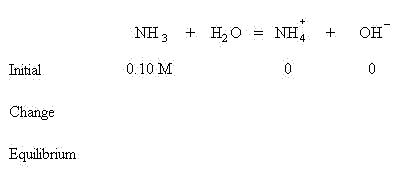
We are assuming that before equilibrium is established, no NH4+ or OH- have formed.
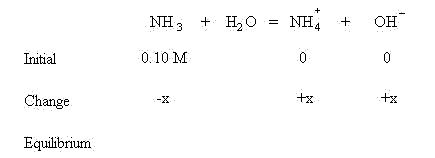
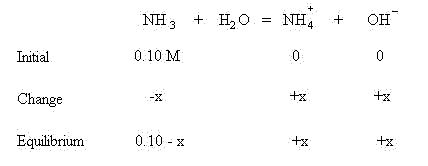
These quantities will be used in the mass action expression:

Let's see if we can neglect the x in the denominator. The last decimal place in 0.10 is to the magnitude of10-2. The magnitude of the constant is 10-5. The difference in magnitude is 103. Since this difference is greater than 100, the x may be neglected. This simplifies the mathematical expression to:

Multiplying both sides of the equation by the denominator yields:
Taking the square root of both sides yields:
To find the pH, first find the pOH by taking the negative log of the hydroxide ion concentration:
Then subtract the pOH from 14 to find the pH:
Buffer Problems
Acidic Buffers

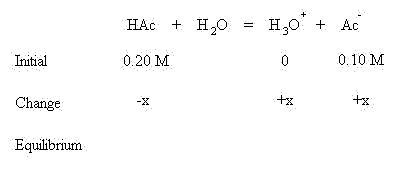
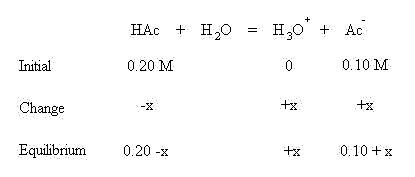
These algebraic quantities may now be inserted into the mass action equilibrium expression for acetic acid:

The values of x shown in bold above may often neglected if they can be shown to be negligibly small. Compare the concentrations to the Ka value. In this case the concentrations of the weak acid and its conjugate base are known to the 10-2 place and the Ka is to the 10-5 place. Since the difference in magnitude is greater than 100 (actually 1000 times different), both of this x quantities may be neglected. This simplifies the algebraic expression to:
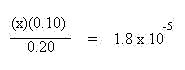
Solving for x gives the hydronium ion concentration:
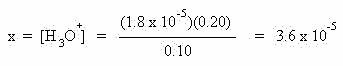
Alkaline Buffers
Begin by forming the table as we have with other acid\ base problems:
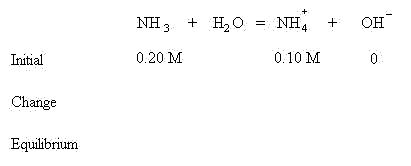
Notice that the concentrations of both weak base and conjugate acid are known. Apply LeChatlier's Principle and see that the equilibrium will shift to the right to create some OH- to establish equilibrium. This means some NH3 will be lost and some additional NH4+ will be formed in addition to some OH-.
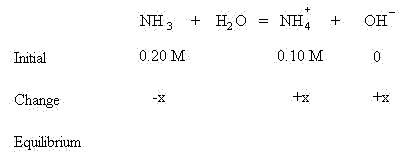
Sum the initial concentrations and the change in concentrations to find the amount of NH3, NH4+ and OH- at equilibrium:
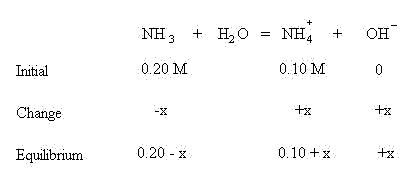
Insert the above expressions into the mass action equilibrium expression:
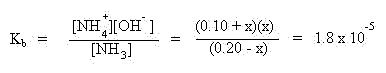
The x quantities shown in bold above often may be neglected. Compare the magnitude of the concentrations of NH3 and NH4+ to the magnitude of Kb. In this case the magnitudes of the concentrations are known to the 10-2 magnitude and the Kb is known to the 10-5 magnitude. Since the difference in magnitude is greater than 100 (difference is 1000), the x quantities shown in bold may be neglected. This simplifies the expression to the expression shown:
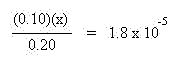
Solve this expression for x which will provide the hydroxide ion concentration:
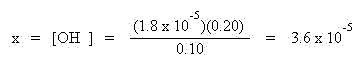
To find the pH, first find the pOH by taking the negative log of the hydroxide ion concentration:
Next, subtract the pOH from 14.00 to find the pH:
Hydrolysis Problems
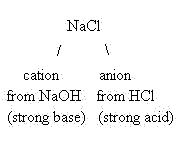
Since the sodium ion came from NaOH, a strong base, this ion is a weak conjugate acid and will not hydrolyze. It will float around in solution as a spectator ion. Likewise, the chloride ion came from HCl, a strong acid. That makes the chloride ion a weak conjugate base and it will not hydrolyze. It also will float around in solution as a spectator ion. As a result, the only hydronium ions present in solution are due to the autoionization of water, and the solution will be neutral in pH.
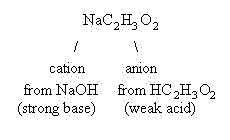
The cation, sodium ion, came from a strong base, NaOH, and as discussed above, will not hydrolyze. However, the anion, acetate ion, came from a weak acid, acetic acid. Acetate ion is therefore a strong conjugate base and will hydrolyze. This means it will behave as a Lowry-Bronsted base, and accept a proton from water, as shown in the equilibrium below:
Notice that hydroxide ion is generated and the salt solution will be alkaline in pH. To calculate the pH of the solution we need to know the initial concentration of the acetate ion (which will be given) and the value of the equilibrium constant, Kb (sometimes labeled as Kh, for hydrolysis constant). The equilibrium constant may be calculated from the Kw of water and the Ka of the weak acid from which the conjugate base forms:
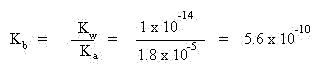

According to LeChatlier's Principle, the reaction will shift to the right to establish equilibrium since there is no acetic acid or hydroxide yet present. This means an x amount of acetate ion will be consumed and an x amount of both acetic acid an hydroxide ion will be formed, as shown in the table below:
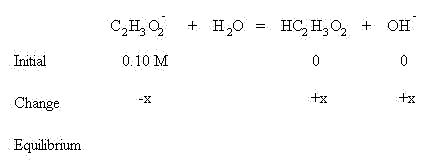
Sum the initial concentrations and the change in concentrations to find the amounts present at equilibrium:

These quantities may by substituted into the mass action expression:

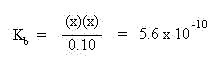
Multiplying both sides of the equation by the denominator, 0.10, yields:
To find x, take the square root of both sides of the equation:
Notice that x corresponds to the hydroxide ion concentration. Now that the hydroxide ion concentration is known, the pH may be found by first calculating the pOH:
The pH may now be found by subtracting the pOH from 14.00:
As shown by the equilibrium, the solution is alkaline.
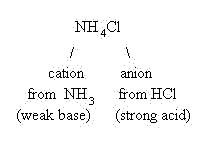
The chloride anion is the weak conjugate base of a strong acid (HCl) and will not hydrolyze. The ammonium cation, however, is the strong conjugate acid of a weak base (NH3) and will hydrolyze--it will act as a Lowry-Bronsted acid and donate a proton to water:
Since hydronium ion is being generated, this solution will be acidic in pH. To calculate the pH of this solution, we need to know the initial concentration of the salt (which will be given), and the equilibrium constant. The equilibrium constant will be calculated in a similar manner as for alkaline salts, using the Kw of water in the Kb of the base from which the conjugate acid formed:
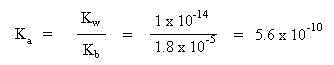
Using an initial concentration of salt to be 0.10 M, set up a table of initial concentrations, change in concentrations and equilibrium concentrations:
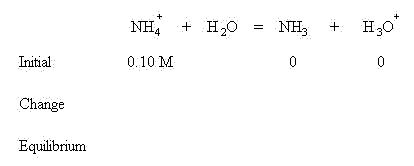
We are assuming that before equilibrium is established, no ammonia or hydronium ion has been produced. In order to establish equilibrium, an x amount of ammonium ion will be lost to form an x amount of ammonia and hydronium ion. This follows LeChatlier's Principle--the reaction will shift to the right to establish equilibrium. The change in concentrations is shown below:
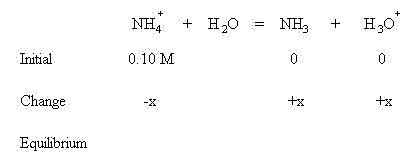
Sum the initial concentrations and change in concentrations to find the concentrations present at equilibrium:
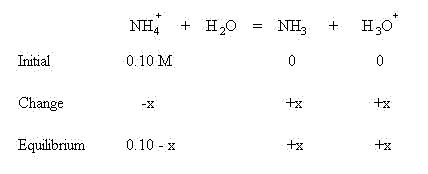
Use the equilibrium concentrations in the mass action expression:

The x amount shown in bold may be neglected since the difference in magnitude between the initial concentration (10-2) and the equilibrium constant (10-10) is 108. This simplifies the above expression to:
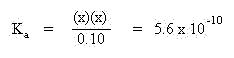
Multiplying both sides of the equation by the denominator, 0.10, yields:
Solve for x by taking the square root of both sides of the equation:
Notice that x is also the hydronium ion concentration. To find the pH take the negative log of the hydronium ion concentration:
As shown by the equilibrium, the solution is acidic.