ELECTROCHEMISTRY

Electrochemistry is the area of chemistry dealing with the interconversion of electrical energy and chemical energy. There are many applications of this in every day life. Batteries, control of corrosion, metallurgy and electrolysis are just a few examples of the applications of electrochemistry. This handout will look at the basic principles of electrochemistry and show some of its applications.

Electrochemistry always involves an oxidation-reduction process. Recall that oxidation involves the loss of electrons by a substance and that reduction involves the gain of electrons by a substance. You can’t have one process without the other. The substance that is reduced is the oxidizing agent. This makes sense, because how you define an oxidizing agent – a compound that is able to oxidize another substance by removing electrons from that substance. Since the oxidizing agent is gaining the electrons that it pulls off the substance it is oxidizing, the oxidizing agent becomes reduced during the process. Similarly, the substance that is oxidized is the reducing agent. A reducing agent is a compound that will reduce another substance by giving away its own electrons to the substance it is reducing. Thus, since the reducing agent is losing those electrons, it becomes oxidized during the process. It is important to be able to determine the oxidation states of the compounds involved in an electrochemical process so as to identify which substance is oxidized and which substance is reduced. If you need help with this, please refer to the handout “Determining Oxidation States” found on this website.

In general, metals tend to make good reducing agents because they can only be oxidized. The reducing ability of the metal is given by the activity series. The more active metal is able to reduce the less active metal cation. This activity series is:

Li>K>Ca>Na>Mg>Al>Zn>Cr>Fe>Ni>Sn>Pb>H₂>Cu>Hg>Ag>Pt>Au

most active least active

So for example, magnesium metal is able to reduce copper(II) ions in solution to form magnesium ions and copper metal:

Mg(s) + Cu²⁺(aq) → Mg²⁺(aq) + Cu(s)

Notice how the very reactive alkali metals are the most active. This makes perfect sense. The alkali metals are very easily oxidized, thus readily want give away its electrons to reduce another substance. On the other hand, metals like copper, gold and silver are among the least active. Due to this property, these metals are often used for coinage and jewelry. You certainly wouldn’t want your coins or jewelry to rust away with time! Other more active metals such as magnesium and zinc are used to protect more active metals, such as iron. Magnesium disks are bolted to ocean-going ships to protect their hulls from corrosion while traversing the ocean. The magnesium corrodes more easily, thus keeps the iron in the hull from rusting. This process is called “cathodic protection”.

Galvanic Cells

A common application of electrochemistry is the galvanic cell, commonly known as a battery. A galvanic cell has the capability of producing a voltage and was invented by Luigi Galvani and Alessandro Volta. A schematic of such a cell is shown below:

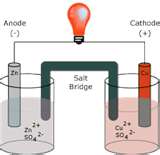
The schematic shows how a zinc anode connected by a salt bridge to a copper cathode will convert chemical energy to electrical energy and allow the light bulb to light up. Lets look at the electrochemistry involved. For any electrochemical cell, oxidation always occurs at the anode and reduction always occurs at the cathode. An easy way to remember this is to keep the vowels together and the consonants together (oxidation at the anode; reduction at the cathode). Also, when drawing a galvanic cell, most people use the convention where the anode is on the left and the cathode is on the right. Use the mnemonic: ABC to remember this convention (Anode/Bridge/Cathode).

Since drawing a galvanic cell isn’t always convenient, a line notation, called cell notation, is often used to describe a galvanic cell. The cell notation for the above cell would be:

Zn(s) | Zn²⁺(aq), 1M; SO₄^2-(1M) || Cu²⁺(aq), 1M; SO₄^2-(1M) | Cu(s)

One begins at the solid zinc anode. A single vertical line indicates a phase change from solid zinc anode to aqueous zinc sulfate solution in the anode compartment. The double vertical line indicates the salt bridge connecting the anode compartment to the cathode compartment. Next, one describes the copper(II) sulfate solution in the cathode compartment. Once again, a single vertical line indicates a phase change from aqueous copper(II) solution in the cathode compartment to the solid copper cathode.

The cell described above is often referred to as a standard cell. The parameters for a standard cell require the species in solution to have a concentration of 1 M, the partial pressure of gases (or more appropriately, the fugacity) to be 1 atm and the temperature to be 25˚C (298K).

Using these standard conditions, we can describe a standard electrode potential, having a symbol, E˚, in volts and make it possible to calculate the electrical potential of the cell. The superscript, ˚, denotes standard conditions. You possible have seen this notation prior to this with standard thermodynamic parameters, such as standard enthalpy change, ΔH˚. The standard electrode potentials are usually listed as reduction potentials and are relative to a standard hydrogen electrode (SHE) having a 0 volt potential as a reference point. There are two methods for calculating the cell potential, E˚_cell. I will describe both methods and you can choose the method that works best for you.

Method 1

This is probably the most common method. Since all the electrode potentials are listed as reduction potentials, the cell potential is calculated directly form the table using the equation:

E˚_cell = E˚_cathode - E˚_anode

Let’s find the cell potential for the galvanic cell we diagramed earlier. First, let’s write out the half cell reactions. One half cell reaction will show the oxidation and the other half cell reaction will show the reduction. Recall oxidation occurs at the anode and reduction at the cathode.

anode (oxidation) Zn(s) → Zn²⁺(aq) + 2 eˉ

cathode (reduction) Cu²⁺(aq) + 2 eˉ → Cu(s)

Cell reaction Zn(s) + Cu²⁺(aq) → Zn²⁺(aq) + Cu(s)

(notice that sulfate is not include, since it is a spectator ion)

Go to any standard textbook, chemical reference book, or a reliable internet site and find a table of standard reduction potentials.

The reduction potential for Zn²⁺(aq) + 2 eˉ → Zn(s) is –0.76 V and the reduction potential for Cu²⁺(aq) + 2 eˉ → Cu(s) is 0.34 V. Using these reduction potentials, calculate the cell potential:

E˚_cell = E˚_cathode - E˚_anode = 0.34 V – (-0.76 V) = +1.10V

Method 2

This is an alternative method that uses more of a “logic” approach. Once again, the oxidation and reduction half cell reactions are used. The sign on the reduction potential for the oxidation half reaction is changed to make it become an actual oxidation potential. In the problem we have been working, the actual half reaction for zinc is an oxidation: Zn(s) → Zn²⁺(aq) + 2 eˉ. The half cell potential for the oxidation would be +0.76 V. The cell potential becomes the sum of the reduction potential and the oxidation potential:

E˚_cell = E˚_red + E˚_ox

Thus in our problem:

E˚_cell = E˚_red + E˚_ox = 0.34V + 0.76 V = +1.10V

An E˚ > 0 means the cell will be spontaneous (produce a voltage). An E˚ < 0 means the cell must be supplied that voltage from an external power supply in order for the cell reaction to run in the direction it is written. If anything, that cell would want to run in the reverse direction. Often these nonspontaneous cells are called electrolytic cells. We will see a mathematical equation that relates cell potential and spontaneity as well as look at an example of an electrolytic process later in this handout.

What happens when the cell is not under standard conditions? The Nernst equation will have to be applied under nonstandard conditions:

where E_cell = nonstandard cell potential in volts

E˚_cell = standard cell potential in volts

R = constant, 8.314 J/mol·K

T = temperature in Kelvin

n = moles of electrons transferred

F = Faraday’s constant = 96485 C/mol eˉ

note: C represents the coulombs (unit of charge)

Q = the reaction quotient expression

Alternative representations of the Nernst Equation may be used if the temperature is standard temperature (298K) and one has a choice of natural logarithm (ln) or common logarithm, base 10 (log):

Let’s modify our previous cell as follows:

Zn(s) | Zn²⁺(aq), 3.00M; SO₄^2-(3.00M) || Cu²⁺(aq), 0.0015M; SO₄^2-(0.0015M) | Cu(s)

We already have E˚_cell = +1.10V. Let the temperature be standard (298K). The Nernst equation expression becomes:

Evaluating the above expression gives:

E_cell = +1.10 V – 0.098 V = 1.00 V

Cell potentials have many other uses. As mentioned earlier, the cell potential indicates whether the cell reaction is spontaneous or nonspontaneous. If you recall, spontaneity for a process is often associated with its Gibbs free energy change, ΔG. There is a mathematical relationship between cell potential and this Gibbs free energy change:

ΔG˚ = – nFE˚ under standard conditions

ΔG = – nFE under nonstandard conditions

where ΔG = change in Gibbs free energy in Joules

n = moles of electrons transferred

F = Faraday’s constant = 98485 C/mol e^-

E = cell potential

Using the units of Faraday’s constant, coulombs/mol e^- and volts for cell potential, the Gibbs free energy units would work out to coulomb-volts. Interestingly enough, the units, coulomb-volts, are equivalent to Joules!

Let’s calculate the Gibbs free energy change for the nonstandard cell we described in the previous problem:

ΔG = – nFE = – (2 mol e^-)(96485 C/mol e^-)(1.00 V) = – 1.94 x 10⁵ J

Let’s quickly review some thermodynamics to see how other information may be obtained from the Gibbs free energy change.

If you recall from thermodynamics:

ΔG = ΔG˚ + RTlnQ

At equilibrium, ΔG = 0, thus Q becomes K_eq and the expression simplifies to:

ΔG˚ = – RTlnK_eq

Now that the Gibbs free energy is known, it can be related to the equilibrium constant, as well as the cell potential:

ΔG˚ = – nFE˚ = – RTlnK_eq

So if we wanted to know the equilibrium constant value for our standard cell, it can be easily calculated:

ΔG˚ = –RTlnK_eq

– 1.94 x 10⁵ J = – (8.314 J/mol·K)(298 K) lnK_eq

Solving for lnK_eq:

Take the antilog to find K_eq:

The large value for K_eq indicates the reaction will proceed significantly towards products.

Electrolysis

The electrolysis process is often used to extract and purify metals from their molten salt form. A current is applied to the molten salt for a period of time. Here is a quick review of the physics before we go further. Current is measured in amperes, A. An ampere is equivalent to the coulombs of charge per second, C/s. In other words:

Let’s suppose you are trying to purify aluminum from a melt containing aluminum cations. If a current of 5.00 A is used for 2 hours, how many grams of aluminum metal can be extracted?

For every mole of Al³⁺ cations, 3 moles of electrons are gained to form 1 mole of aluminum metal: Al³⁺ + 3 e^- → Al

The rest is getting the units to work out!

© Copyright, 2001, L. Ladon. Permission is granted to use and duplicate these materials for non-profit educational use, under the following conditions: No changes or modifications will be made without written permission from the author. Copyright registration marks and author acknowledgement must be retained intact.