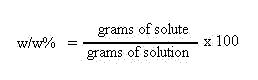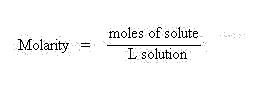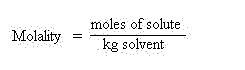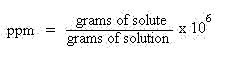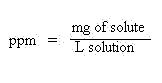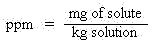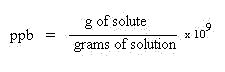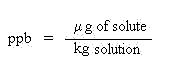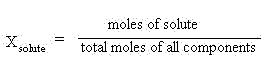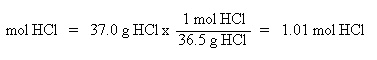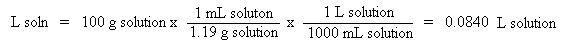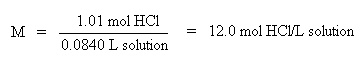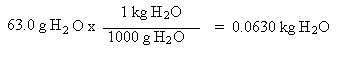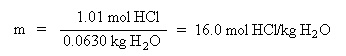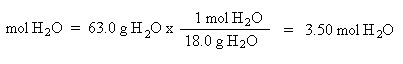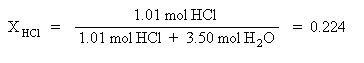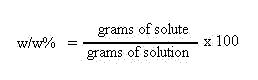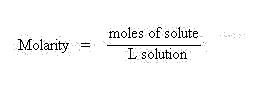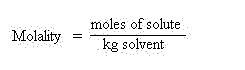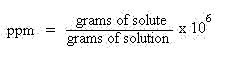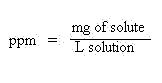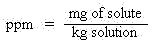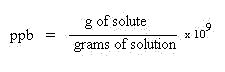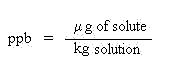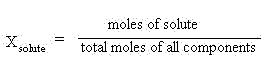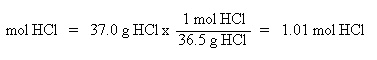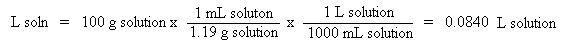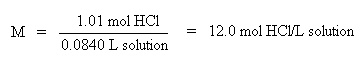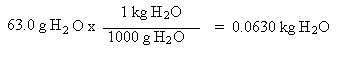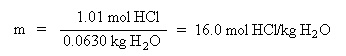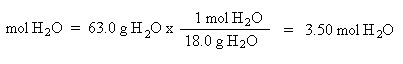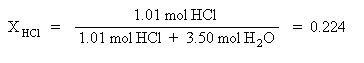CONCENTRATION UNITS

This handout will deal with units of concentration and how to convert from one concentration unit to another. It will be important to understand a few terms dealing with solutions, so let's define them:

Solution -- a mixture consisting of a solute and a solvent
Solute -- component of a solution present in the lesser amount
Solvent -- component of a solution present in the greater amount
Concentration -- amount of a solute present in a solution per standard amount of solvent

There are numerous ways of expressing concentrations. It will be important to know the units used to express each concentration, as these units essentially define the concentration. Let's look at some ways to express concentration.

Weight/Weight Percent (w/w%): This unit of concentration is often used for concentrated solutions, typically acids and bases. If you were to look on a bottle of a concentrated acid or base solution the concentration expressed as a weigh/weight percent. A weight/weight percent is defined as:

Molarity (M): This unit of concentration relates the moles of solute per liter of solution.


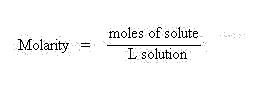
Molarity is the most common concentration unit involved in calculations dealing with volumetric stoichiometry.

Molality (m): This unit of concentration relates the moles of solute per kilogram of solvent.


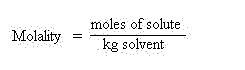
Molality is often used as the concentration unit involved in calculations dealing with colligative properties, such as freezing point depression, boiling point elevation and osmotic pressure.

Parts per million (ppm): This unit of concentration may be expressed in a number of ways. It is often used to express the concentration of very dilute solutions. The "technical" definition of parts per million is:

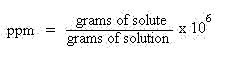
Since the amount of solute relative to the amount of solvent is typically very small, the density of the solution is to a first approximation the same as the density of the solvent. For this reason, parts per million may also be expressed in the following two ways:



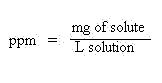
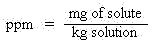
Parts per billion (ppb): This concentration unit is also used for very dilute solutions. The "technical" definition is as follows:

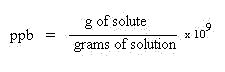Owing to the dilute nature of the solution, once again, the density of the solution will be about the same as the density of the solvent. Thus, we may also express parts per billion as:



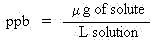
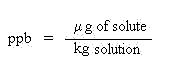
Mole fraction (X) and mole percent (%X): A fraction is defined as a part over a whole. Multiplying this fraction by 100 would give the percent. Thus, a mole fraction involves knowing the moles of solute or component of interest over the total moles of all components in the solution mixture:


You may find it necessary to be able to convert from one concentration unit to another. The key to solving this type of problem is to realize that you may make an assumption to get started. You may need to know the density of the solution, which would be given in the problem. Then, by using dimensional analysis, you try to get to the units of the concentration unit you are seeking to find. To get started, assume the quanitity of solution found in the denominator unit of the concentration unit you are trying to convert. For example, if you are trying to convert weight/weight percent to molarity, assume 100 grams of solution. If you are trying to convert molarity to weight/weight percent, assume 1 liter of solution.

Let's look at a typical example. Suppose you are given a concentrated solution of HCl which is known to be 37.0% HCl and has a solution density of 1.19 g/mL. What is the molarity, molality and mole fraction of HCl?

Begin with the assumption of 100 g of solution. With this assumption, you now know a few other facts. In 100 g of solution, 37.0 g is due to HCl (grams of solute) and 63.0 g is due to water (grams of solvent).

To find molarity, we need to determine the moles of HCl (solute) per liter of solution. First, convert the known amount of HCl (37.0 g) to moles:


Next, convert the known mass of solution, 100 g solution, to liters of solution, using the density of the solution:


Since the moles of solute (HCl) and volume of solution in liters is now know, calculate the molarity (M) as the moles of solute per liter of solution:


From the information above, let's find the molality of the HCl solution. The moles of solute is already known (1.01 mol HCl). We need to find the kilograms of solvent:


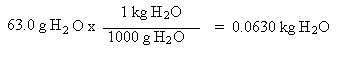
Since molality (m) is defined as the moles of solute per kilogram solvent, it becomes easy to find the molality:

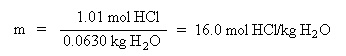
Finally, let's tackle the mole fraction of HCl. The moles of HCl is known to be 1.01 mole. We need to find the moles of H2O:


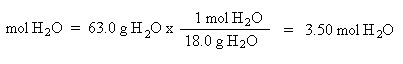
Since the moles of solute (HCl) and moles of solvent (H2O) are known, the mole fraction of HCl may be calculated:

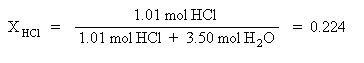
This concludes the tutorial!

Created With HTML Assistant Pro - 05/11/2001 © Copyrght, 2001, L. Ladon. Permission is granted to use and duplicate these materials for non-profit educational use, under the following conditions: No changes or modifications will be made without written permission from the author. Copyright registration marks and author acknowledgement must be retained intact.