CHEMICAL EQUILIBRIA

Many chemical reactions involve an equilibrium process. During an dynamic equilibrium, the rate of the forward reaction equals the rate of the reverse reaction. This means that both reactants and products will be present at any given point in time. The equilibrium may favor either the reactants or products. The extent to which the reaction proceeds towards products is measured by an equilibrium constant. This constant is a specific ratio of the products to the reactants. This ratio is often referred to as a mass action expression. Let's look at a "generic" equilibrium reaction and its mass action expression.


The mass action expression consists of the product of the products, each raised to the power given by the coefficient in the balanced chemical equation, over the product of the reactants, each raised to the power given by the coefficient in the balanced chemical equation. This mass action expression is set equal to the equilibrium constant, Keq:


There are numerous types of equilibrium problems one may encounter, both qualitative and quantitative. In the subsequent pages we will look at these various types of problems.

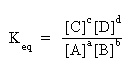
Qualitative Problems

Qualitatively, one may look at how far an equilibrium lies towards the right (towards products) or left (towards reactants). The magnitude of the equilibrium constant gives one a general idea of whether the equilibrium favors products or reactants. If the reactants are favored, then the denominator term of the mass action expression will be larger than the numerator term, and the equilibrium constant will be less than one. If the products are favored over the reactants, then the numerator term will be larger than the denominator term, and the equilibrium constant will be greater than one. The following two equilibria, demonstrate a case in which the reactants are favored and a case in which the products are favored. Note the magnitude of the equilibrium constant for each example:


An equilibrium is able to shift in either direction, either towards reactants or towards products, when a stress is placed on the equilibrium. This stress may involve increasing or decreasing the amount of a reactant or product, changing the volume or pressure in gas phase equilibria or changing the temperature of the equilibrium system. The direction in which the equilibrium shift may be predicted by using Le Chatlier's Principle. Le Chatlier's Principle states that if a stress is placed on an equilibrium, the equilibrium will shift in the direction which relieves the stress. Let's look at an equilibrium and the direction it will shift due to various stresses placed on it.

2 N2 (g) + 3 H2 (g) 2 NH3 (g)

Suppose additional nitrogen (N2) was added to the system. First, identify the stress. The stress is too much nitrogen. The equilibrium will shift to the right, towards products, in order to remove the excess nitrogen.

Suppose some ammonia (NH3) was removed from the system. The stress is not enough ammonia, so the equilibrium will shift to the right to replenish the ammonia removed.

Suppose some hydrogen (H2) was removed from the system. The stress is not enough hydrogen, so the equilibrium will shift to the left to replenish the hydrogen removed.

Suppose the pressure is increased. The stress is too much pressure. In this case, the only way to relieve the stress is to reduce the pressure. How may this be done? The pressure in the container is due to the number of gas particles hitting the sides of the container with given force. A reduction in the number of particles will cause the pressure to drop. Upon examining the equilibrium, one sees that there are five moles of gas particles on the left hand side of the equilibrium, while there are two moles of gas particles on the right hand side of the equilibrium. Thus if the equilibrium shifts to the right, the number of gas particles in the container become reduced, and the excess pressure is relieved.

Suppose a catalyst is added to the system. Since the catalyst is not a part of the equilibrium, the equilibrium will not shift. The only affect that a catalyst has on an equilibrium is to allow the system to reach equilibrium faster.

Suppose an inert gas, such as helium, as added to the system. Since helium is not a part of this equilibrium, it will not affect the equilibrium.

It is important to note that the value of the equilibrium constant has not changed when the above stresses were placed on the equilibrium. It is, after all, a constant. The only factor which will affect the value of the equilibrium constant is temperature. In fact, you will note that when an equilibrium constant is cited, the temperature at which that constant holds true is also cited. Thus if the temperature is changed, the equilibrium shift will be accompanied by a change in the value of the equilibrium constant.
Suppose you know that the following equilibrium is exothermic ( H < 0):

H2 (g) + Cl2 (g) 2 HCl (g) Keq = 4 x 1031 at 300 K

Since the process is exothermic, heat is released by the system to the surroundings, so one may include heat in the equilibrium as a product:

H2 (g) + Cl2 (g) 2 HCl (g) + heat

Suppose the temperature of the system is increased to 500 K. The stress is too much heat, so the equilibrium will shift to the left to remove the excess heat. In addition, the value of the equilibrium constant decreases to 4 x 1018 , indicating the equilibrium lies further to the left.

When writing the mass action expression of an equilibrium, only include the components in the equilibrium which are in the same phase. Never include solids. Let's look at some equilibrium reactions involving more than one phase, and their mass action expressions.

CaCO3 (s) CaO(s) + CO2(g)

Keq = [CO2]

Notice that the solids were not included as part of the mass action expression.

HCl(aq) + CaCO3 (s) CaCl2 (aq) + CO2 (g)


Notice that the equilibrium mass action expression may be expressed in two ways; Keq1 is expressed in terms of the concentrations of the aqueous species, while Keq2 is expressed in terms of the concentration of the gaseous species. These two constants will have different values. Which expression do you use? That depends on the information given in the problem. If the concentrations of the aqueous species are given, use the expression for Keq1 . If the concentration for CO2 is given, use the expression for Keq2 . Realistically, one uses the expression whose quantities are most easily measured experimentally. The main idea is not to mix phases, and that the solid is not included in either expression.

Quantitative Problems

Next, let's consider some quantitative problems dealing with chemical equilibria. By examining the amounts of reactants and products at equilibrium, one may numerically see how an equilibrium favors either reactants or products.

Suppose we are given the following equilibrium at 500 K:

CO(g) + 2 H2 (g) CH3OH(g)

The equilibrium concentrations are: [CO] = 0.0911 M, [H2] = 0.0822 M, [CH3OH] = 0.00892 M, what is the value of the equilibrium constant? Does the equilibrium favor reactants or products?

First, we need to write the mass action expression:


Next, substitute the equilibrium concentrations into the mass action expression, and calculate for the equilibrium constant:


Since the value of the equilibrium constant is greater than one, (Keq >1), the equilibrium favors the products.

Another type of equilibrium problem deals with finding the equilibrium concentrations given the initial concentrations and the value of the equilibrium constant. Suppose you are given the following equilibrium:

CO(g) + H2 O(g) CO2 (g) + H2 (g) Keq = 23.2 at 600 K

If the initial amounts of CO and H2O were both 0.100 M, what will be the amounts of each reactant and product at equilibrium?

For this type of problem, it is convenient to set a table showing the initial conditions, the change that has to take place to establish equilibrium and the final equilibrium conditions. Let's begin by showing the initial conditions:


Initially, 0.100 M CO and 0.100 M H2O are present. Equilibrium hasn't been established yet, so the amounts of CO2 and H2 are assumed to be zero.

To establish equilibrium, some CO and H2O has to react, so we will call the amount of CO and H2O reacted x, and the same x amount of CO2 and H2 must form:


The amounts of reactants and products present at equilibrium will be the combination of the initial amounts and the change. Just add the quantities together:


Substitute the above algebraic quantities into the mass action expression:


Since the algebraic expression is a perfect square, begin solving for x by taking the square root of both sides of the equation:



Multiply both sides by the denominator, 0.100 - x:


The term, 0.100 - x, cancels out on the left hand side, and the term, 4.85 must be distributed through the term 0.100 - x on the right hand side:

x = 0.485 - 4.85x

Add 4.85x to both sides of the equation:

x + 4.85x = 0.485 - 4.85x + 4.85 x

Combining terms:

5.85x = 0.485

Solve for x by dividing both sides by 5.85:

Recall that x represents the equilibrium quantities of both H2 and CO2 . The equilibrium quantities of CO and H2O is given by:

0.100 - x = 0.100 - 0.0829 = 0.017 M = [CO] = [H2O]

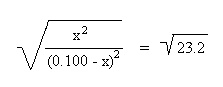
© Copyright, 2001, L. Ladon. Permission is granted to use and duplicate these materials for non-profit educational use, under the following conditions: No changes or modifications will be made without written permission from the author. Copyright registration marks and author acknowledgement must be retained intact.